具体来说我们什么时候选择考虑单调栈呢,答案是,通常是一位数组需要寻找一个元素的左边或者右边比自己大或者小的第一个元素的位置。
单调栈中的元素存的是元素的位置。
直白的来说,单调栈使用栈来记录一遍我们遍历过的元素的位置,一旦遍历元素的值大于栈顶的值,则栈顶元素右边比自己大的第一个元素的位置就是遍历元素的位置,然后栈顶元素需要出栈。
至于为什么叫单调栈,因为栈顶到栈底是有序的,如果是找一个元素右边第一个更大元素,则栈顶到栈底的顺序为递增。
每日温度
给定一个整数数组temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& T) {
stack<int> st; // 递增栈
vector<int> result(T.size(), 0);
for (int i = 0; i < T.size(); i++) {
while (!st.empty() && T[i] > T[st.top()]) { // 注意栈不能为空
result[st.top()] = i - st.top();
st.pop();
}
st.push(i);
}
return result;
}
};下一个更大元素 I
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
需要关注的点:
- 1 nums1是nums2的子集
- 2 对应位置 – 哈希表
- 3 更大元素 – 单调栈
求解方法:
- 1 首先我们先求出nums2数组的下一个更大元素数组。
- 2 其次建立一个nums1中元素-索引的哈希表{“元素”:索引}。
- 3 遍历nums2,找到nums1中元素的索引位置。
哈希表也可以继续使用nums2构建,都可以。
class Solution {
public:
vector nextGreaterElement(vector& nums1, vector& nums2) {
unordered_map<int, int> map;
stack st;
int m = nums1.size(), n = nums2.size();
vector result(m, -1);
vector vec(n, -1);
// 1 求解nums2的更大元素数组
st.push(0);
for(int i=1; i<n; i++){ while(!st.empty() && nums2[i] > nums2[st.top()]){
vec[st.top()] = nums2[i];
st.pop();
}
st.push(i);
}
// 2 使用nums1的值和索引构建哈希表
for(int i=0; i<m; i++){
map[nums1[i]] = i;
}
// 3 nums2的值去map中查询得到nums1的索引
for(int i=0; i<n; i++){
if (map.count(nums2[i])) result[map[nums2[i]]] = vec[i];
}
return result;
}
};
下一个更大元素 II
给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。
数字 x 的 下一个更大的元素 是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1 。
在上一题的基础上,数组变成循环数组。
最简单的做法就是将nums拼接,然后找下一个更大元素。最后删除多余的数组。
class Solution {
public:
vector find_next_element(vector& nums)
{
vector result(nums.size(), -1);
stack st;
st.push(0);
for(int i=1; i<nums.size(); i++) { while(!st.empty() && nums[i] > nums[st.top()])
{
result[st.top()] = nums[i];
st.pop();
}
st.push(i);
}
return result;
}
vector nextGreaterElements(vector& nums) {
vector result;
vector new_nums;
for(int i=0; i<2*nums.size(); i++)
{
new_nums.push_back(nums[i%nums.size()]);
}
result = find_next_element(new_nums);
for(int i=0; i<nums.size(); i++)
{
result.pop_back();
}
return result;
}
};
class Solution {
public:
vector build_stack(vector& nums)
{
stack st;
vector result(nums.size(), -1);
st.push(0);
int j;
for(int i=1; i< 2*nums.size(); i++)
{
j = i % nums.size();
while(!st.empty() && nums[j] > nums[st.top()])
{
result[st.top()] = nums[j];
st.pop();
}
st.push(j);
}
return result;
}
vector nextGreaterElements(vector& nums) {
int m = nums.size();
vector result;
result = build_stack(nums);
return result;
}
}; 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
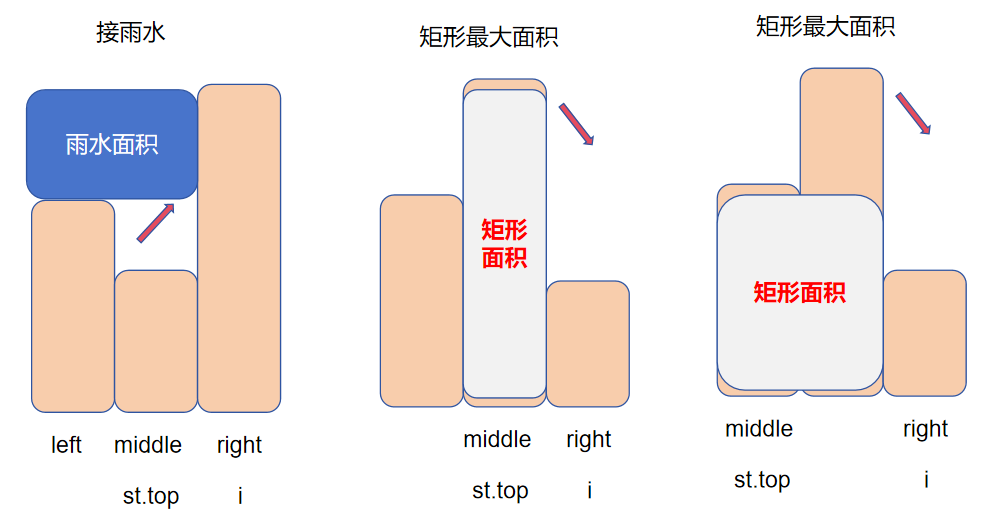
接雨水不同于上述几道题只需要控制栈顶和遍历到的元素即可,接雨水同时需要控制栈顶元素,栈顶左边的元素和当前遍历元素。
解题思路:
- 1 该题使用单调栈来找到栈顶元素的左右两边的更大元素,进而计算夹在左右两边更大元素中横向方块的雨水面积。
- 2 横向方块的高 = 当前遍历元素和的栈顶左边元素最小值-栈顶元素。
- 3 横向方块的宽 = 当前遍历元素的索引-栈顶左边元素的索引-1
class Solution {
public:
int trap(vector<int> &height) {
int result = 0;
stack<int> st;
for(int i = 0; i<height.size(); i++){
while(!st.empty() && height[i] > height[st.top()]){
// 1 找中间元素
int middle = st.top(); st.pop();
// 2 找左边元素
if (!st.empty()){
// 3 计算中间面积
int h = min(height[i], height[st.top()]) - height[middle];
int w = i - st.top() - 1;
result += w * h;
}
}
st.push(i);
}
return result;
}
};柱状图中最大的矩形
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
输入:heights = [2,1,5,6,2,3] 输出:10 解释:最大的矩形为图中红色区域,面积为 10
解题思路:
- 1 和接雨水类似,都需要找到栈顶元素,栈顶左边元素,当前遍历元素3个值进行求解。
- 2 该题的计算模式需要栈顶左边元素,栈顶元素,当前遍历元素的关系为:大,大大,小。
- 3 所求矩形面积宽为middle到right的距离*middle的高。
- 4 为了处理单个元素,需要在数组的开头和末尾插入0元素。
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> st;
// 这样单个元素也可以得到处理
heights.insert(heights.begin(), 0); // 数组头部加入元素0
heights.push_back(0); // 数组尾部加入元素0
int result = 0;
for (int i = 0; i < heights.size(); i++) {
while (!st.empty() && heights[i] < heights[st.top()]) {
int mid = st.top(); st.pop();
if (!st.empty()){
int w = i - st.top() - 1;
int h = heights[mid];
result = max(result, w * h);
}
}
st.push(i);
}
return result;
}
};最大矩形
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例 1:
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] 输出:6 解释:最大矩形如上图所示。
解题思路:
- 1 该题从题目描述来说,很像最大正方形(动态规划),但是由于其没有正方形的限制,无法组织递归方程,实际上该题是柱状图中最大的矩形题目的魔改版。
- 2 首先需要获取自底向上的一维高度作为柱状图,然后使用N次柱状图最大的矩阵的题目解法即可。
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> st;
// 这样单个元素也可以得到处理
heights.insert(heights.begin(), 0); // 数组头部加入元素0
heights.push_back(0); // 数组尾部加入元素0
int result = 0;
for (int i = 0; i < heights.size(); i++) {
while (!st.empty() && heights[i] < heights[st.top()]) {
int mid = st.top(); st.pop();
if (!st.empty()){
int w = i - st.top() - 1;
int h = heights[mid];
result = max(result, w * h);
}
}
st.push(i);
}
return result;
}
int maximalRectangle(vector<vector<char>>& matrix) {
vector<vector<int>> heights;
int result = 0;
int m = matrix.size(), n = matrix[0].size();
// 1 获取柱状图
for(int i=0; i<m; i++){
vector<int> height(n, 0);
// 列
for(int j=0; j<n; j++){
// 行
for(int k=m-1-i; k>=0; k--){
if (matrix[k][j] - '0') height[j]++;
else break;
}
}
for(auto h:height) cout << h << "\t";
cout << endl;
heights.push_back(height);
}
// 2 获取柱状图最大面积
for (auto height:heights){
result = max(result, largestRectangleArea(height));
}
return result;
}
};接雨水VS矩形最大面积