链表中的双指针目前可以分为3类题目:
- 1 两个链表之间的交点
- 1.1 O(n)的空间复杂度,哈希表
- 1.2 O(1)的空间复杂度,快慢指针
- 2 查找链表的某个节点
- 2.1 快慢指针,快指针优先走n部,再快慢指针同步走
- 3 链表的合并和分解
- 3.1 链表的合并,使用两个指针指向待合并的链表
- 3.2 链表的分解,使用两个指针指向分解后的链表
1 两个链表之间的交点
1.1 相交链表
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
解题思路:
- 1 可以遍历一下链表A和链表B的长度,使遍历A,B链表时做长度对齐,如上图所示让链表A从a1开始,链表B从b2开始。
- 2 即,短链表从开头开始遍历,长链表从倒数第N(短链表的长度)个节点开始遍历。
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int lenA = 0, lenB = 0;
ListNode* curA = headA, * curB = headB;
// 1 计算不同链表的长度
while(curA){
curA = curA->next;
lenA++;
}
while(curB){
curB = curB->next;
lenB++;
}
// 2 对齐需要对比的长度
curA = headA;
curB = headB;
if (lenA > lenB){
int n = lenA - lenB;
while(n--) curA = curA->next;
}else{
int n = lenB - lenA;
while(n--) curB = curB->next;
}
// 3 找到相交节点
while(curA){
if (curA == curB) return curA;
else{
curA = curA->next;
curB = curB->next;
}
}
return nullptr;
}
};1.2 环形链表
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:

输入:head = [3,2,0,-4], pos = 1 输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。
解题思路:
- 1 慢指针走一步,快指针走两步,如果有环则快慢指针会相遇。
- 2 如果快指针走到空了,则没有环。
2 查找链表的某个节点
2.1 删除链表的倒数第 N 个结点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
输入:head = [1,2,3,4,5], n = 2 输出:[1,2,3,5]
解题思路 – 快慢指针:
- 1 可以让快指针先走n步,然后快慢指针一起走,当快指针->next变成nullptr时,慢指针的位置为需要删除的节点的前一个节点。
- 2 使用虚拟头结点的话,即快指针先走n+1步
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
// 0 如果需要增加和删除则使用虚拟头结点
ListNode* dummy = new ListNode(0);
dummy->next = head;
ListNode* slow = dummy, * fast = dummy;
n++;
// 1 快指针先走
while(n--) fast = fast->next;
// 2 快慢指针一起走
while(fast){
fast = fast->next;
slow = slow->next;
}
// 3 删除指定元素
ListNode* temp = slow->next;
slow->next = slow->next->next;
delete temp;
return dummy->next;
}
};2.2 单链表的中点
给你单链表的头结点 head ,请你找出并返回链表的中间结点。
如果有两个中间结点,则返回第二个中间结点。
示例 1:

输入:head = [1,2,3,4,5] 输出:[3,4,5] 解释:链表只有一个中间结点,值为 3 。
解题思路:
- 1 快指针走两步,慢指针走一步
class Solution {
public:
ListNode* middleNode(ListNode* head) {
ListNode* slow = head, * fast = head;
while(fast && fast->next){
slow = slow->next;
fast = fast->next->next;
}
return slow;
}
};3 链表的合并和分解
3.1 合并两个有序链表
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
输入:l1 = [1,2,4], l2 = [1,3,4] 输出:[1,1,2,3,4,4]
解题思路:
- 1 使用p1指针指向l1,p2指针指向l2,新链表使用p1和p2中较小的那个。
- 2 一旦某个链表遍历完成,直接将新链表指向还未遍历完成的链表即可。
class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
ListNode* dummy = new ListNode(0);
ListNode* cur = dummy;
ListNode* p1 = list1, *p2 = list2;
// 1 两个链表择最小的加入新链表
while(p1!=nullptr && p2!=nullptr){
if (p1->val < p2->val){
cur->next = p1;
// 1.1 p1链表移动
p1 = p1->next;
}
else{
cur->next = p2;
// 1.2 p2链表移动
p2 = p2->next;
}
// 1.3 新链表移动
cur = cur->next;
}
// 2 把剩下的一条链表直接接到新链表之后
if (p1 == nullptr && p2!=nullptr) cur->next = p2;
else if (p1 != nullptr && p2 == nullptr) cur->next = p1;
return dummy->next;
}
};3.2 单链表的分解
给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
你应当 保留 两个分区中每个节点的初始相对位置。
示例 1: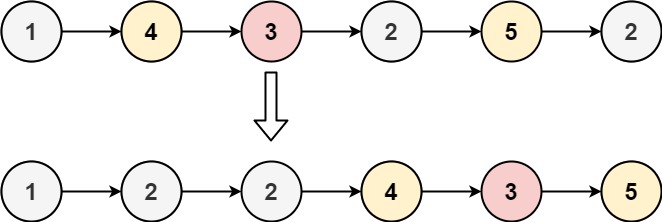
输入:head = [1,4,3,2,5,2], x = 3 输出:[1,2,2,4,3,5]
解题思路:
- 1 使用两个虚拟头结点分别表示两个分离链表,同时使用两个遍历指针指向虚拟头结点。
- 2 将原始链表全部拆解完成后,拼接一下分离后的链表
- 3 每次分离操作都需要释放一下原链表的cur->next的指针,防止成环。
class Solution {
public:
ListNode* partition(ListNode* head, int x) {
// 需要新表就需要设置dummy节点和p=dummy的遍历节点
ListNode* dummy1 = new ListNode(0);
ListNode* dummy2 = new ListNode(0);
ListNode* p1 = dummy1, * p2 = dummy2;
// 原链表的遍历节点
ListNode* cur = head;
while(cur){
if (cur->val < x){
p1->next = cur;
p1 = p1->next;
}
else{
p2->next = cur;
p2 = p2->next;
}
// 释放当前cur->next,防止出现环
ListNode* temp = cur->next;
cur->next = nullptr;
cur = temp;
// cur = cur->next;
}
p1->next = dummy2->next;
return dummy1->next;
}
};3.3 合并k个有序链表
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]] 输出:[1,1,2,3,4,4,5,6] 解释:链表数组如下: [ 1->4->5, 1->3->4, 2->6 ] 将它们合并到一个有序链表中得到。 1->1->2->3->4->4->5->6
解题思路:
- 1 该题相比合并2个有序链表,需要每次对k个有序链表的头结点进行排序,找到最小的头结点。
- 2 该题可以使用优先队列来解决排序的问题,优先队列会维护一个堆,每次加入一个新数据,就会重新调整堆,使堆的top元素为最大或者最小。
- 3 C++中优先队列的使用:
- priority_queue<ListNode*, vector<ListNode*>, function<bool(ListNode*, ListNode*)>> pq([](ListNode* a, ListNode* b){return a->val > b->val;});
详细代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
ListNode* dummy = new ListNode(0);
ListNode* cur = dummy;
priority_queue<ListNode*, vector<ListNode*>, function<bool(ListNode*, ListNode*)>> pq([](ListNode* a, ListNode* b){return a->val > b->val;});
// 1 将每一个链表的头结点压入优先队列
for(auto head:lists){
if (head != nullptr) pq.push(head);
}
// 2 每从优先队列中取出一个节点,就从对应节点的链表后一个节点压入优先队列
while(!pq.empty()){
// 2.1 从优先队列中取出一个节点
ListNode* node = pq.top(); pq.pop();
// 2.2 加入新链表
cur->next = node;
// 2.3 从对应节点的链表后一个节点压入优先队列
if (node->next != nullptr) pq.push(node->next);
// 2.4 更新cur
cur = cur->next;
}
return dummy->next;
}
};
