前缀和/差分数组属于数组类题目中小而美的一类技巧。
1 前缀和
前缀和用于快速、频繁的计算一个索引区间内的元素之和。1.1 区域和检索 – 数组不可变
给定一个整数数组nums,处理以下类型的多个查询:
- 计算索引
left和right(包含left和right)之间的nums元素的 和 ,其中left <= right
NumArray 类:
NumArray(int[] nums)使用数组nums初始化对象int sumRange(int i, int j)返回数组nums中索引left和right之间的元素的 总和 ,包含left和right两点(也就是nums[left] + nums[left + 1] + ... + nums[right])
输入: ["NumArray", "sumRange", "sumRange", "sumRange"] [[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]] 输出: [null, 1, -1, -3]解题思路:
- 1 经典解法:遍历sumRange中的数求和,时间复杂度O(n),空间复杂度O(1)。
- 2 前缀和解法:使用sumRange左右索引对应的前缀和求差即可,时间复杂度O(1),空间复杂度O(n)。
- 2.1 prefixNum前缀和数组需要多出索引为0的一位(方便初始化);
- 2.2 区间[left, right]的前缀和为prefixNum[right+1]-prefixNum[left];
class NumArray {
public:
vector<int> prefixNum;
NumArray(vector<int>& nums) {
prefixNum = vector<int>(nums.size()+1, 0);
for(int i=0; i<nums.size(); i++){
prefixNum[i+1] = prefixNum[i] + nums[i];
}
}
int sumRange(int left, int right) {
return prefixNum[right+1]-prefixNum[left];
}
};1.2 二维区域和检索 – 矩阵不可变
给定一个二维矩阵matrix,以下类型的多个请求:
- 计算其子矩形范围内元素的总和,该子矩阵的 左上角 为
(row1, col1),右下角 为(row2, col2)。
NumMatrix 类:
NumMatrix(int[][] matrix)给定整数矩阵matrix进行初始化int sumRegion(int row1, int col1, int row2, int col2)返回 左上角(row1, col1)、右下角(row2, col2)所描述的子矩阵的元素 总和 。

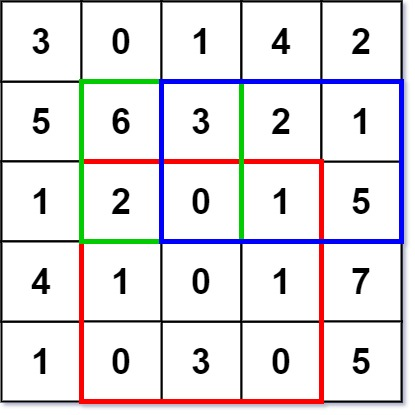
输入: ["NumMatrix","sumRegion","sumRegion","sumRegion"] [[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]] 输出: [null, 8, 11, 12]解题思路:
- 1 二维前缀和数组的大小为(m+1, n+1)
- 2 二维前缀和输出的初始化:
prefixNum[i][j] = prefixNum[i-1][j] + prefixNum[i][j-1] + matrix[i-1][j-1] – prefixNum[i-1][j-1];
- 3 前缀和的计算:
prefixNum[row2+1][col2+1] – prefixNum[row2+1][col1] – prefixNum[row1][col2+1] + prefixNum[row1][col1];
class NumMatrix {
public:
vector<vector<int>> prefixNum;
NumMatrix(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
prefixNum = vector<vector<int>>(m+1, vector<int>(n+1, 0));
for(int i=1; i<=m; i++){
for(int j=1; j<=n; j++){
prefixNum[i][j] = prefixNum[i-1][j] + prefixNum[i][j-1] + matrix[i-1][j-1] - prefixNum[i-1][j-1];
}
}
}
int sumRegion(int row1, int col1, int row2, int col2) {
return prefixNum[row2+1][col2+1] - prefixNum[row2+1][col1] - prefixNum[row1][col2+1] + prefixNum[row1][col1];
}
};2 差分数组
差分数组的适用场景是频繁对原始数组的某个区间的元素进行增减。2.1 航班预定统计
这里有n 个航班,它们分别从 1 到 n 进行编号。
有一份航班预订表 bookings ,表中第 i 条预订记录 bookings[i] = [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti (包含 firsti 和 lasti )的 每个航班 上预订了 seatsi 个座位。
请你返回一个长度为 n 的数组 answer,里面的元素是每个航班预定的座位总数。
示例 1:
输入:bookings = [[1,2,10],[2,3,20],[2,5,25]], n = 5 输出:[10,55,45,25,25] 解释: 航班编号 1 2 3 4 5 预订记录 1 : 10 10 预订记录 2 : 20 20 预订记录 3 : 25 25 25 25 总座位数: 10 55 45 25 25 因此,answer = [10,55,45,25,25]解题思路:
- 1 差分数组的构建:
- 1.1 差分数组的长度与原数组一致
- 1.2 计算方法为difference[i] = nums[i]-nums[i-1];
- 2 差分区间的计算:
- 2.1 若在nums的[left, right]上整体+3,修改差分数组的difference[left]+3和difference[right+1]-3。
- 2.2 计算方法为: nums[i] = nums[i-1] + difference[i];
class Solution {
public:
vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
// 1 构造差分数组
vector<int> difference(n, 0);
vector<int> result(n, 0);
// 2 给差分数组上操作
for(int i=0; i<bookings.size(); i++){
difference[bookings[i][0]-1] += bookings[i][2];
if (bookings[i][1] < n)
difference[bookings[i][1]] -= bookings[i][2];
}
// 3 返回结果
result[0] = difference[0];
for(int i=1; i<n; i++){
result[i] = result[i-1] + difference[i];
}
return result;
}
};