旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:

输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]
解题思路:
- 1 使用额外数组存储(时间复杂度O(n^2),空间复杂度O(n^2))
- 2 不使用额外数组存储(时间复杂度O(n^2),空间复杂度O(1))
1.1 使用额外数组存储
- 顺时针:matrix[j][m-1-i] = temp[i][j];
- 逆时针:matrix[i][j] = temp[j][m-1-i];
class Solution {
public:
void rotate(vector<vector>& matrix) {
vector<vector> temp = matrix;
int m = matrix.size(), n = matrix[0].size();
for(int i=0; i<m; i++){
for(int j=0; j<n; j++){
// 顺时针
matrix[j][m-1-i] = temp[i][j];
// 逆时针
// matrix[i][j] = temp[j][m-1-i];
}
}
}
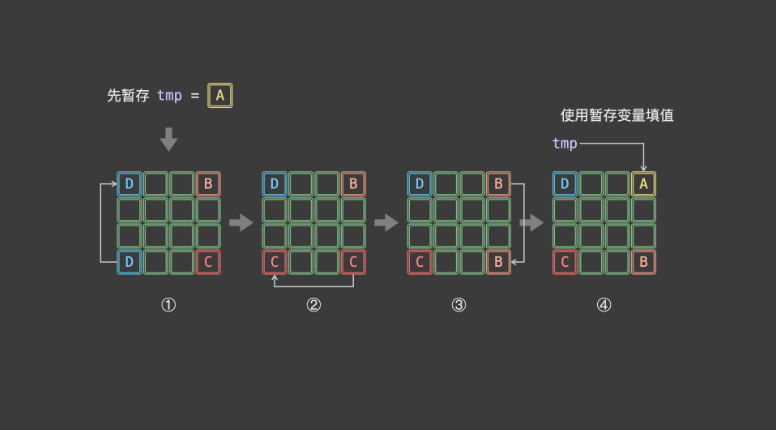
};1.2 不使用额外数组存储
顺时针旋转后:
- 1 后一个元素的列变成了前一个元素的行
- 2 后一个元素的行+前一个元素的行=矩阵长度-1
需要注意的地方:
- 1 逆时针从最左上角反向替换
- matrix[i][j] = matrix[n-1-j][i];
- matrix[n-1-j][i] = matrix[n-1-i][n-1-j];
- matrix[n-1-i][n-1-j] = matrix[j][n-1-i];
- matrix[n-1-i][n-1-j] = matrix[i][n-1-j]
- matrix[j][n-1-i] = temp;
- 2 注意奇数矩阵和偶数矩阵
- 奇数矩阵:行:0 ~ n/2 列:0 ~ (n+1)/2
- 偶数矩阵:行:0 ~ n/2 列:0 ~ (n)/2
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
for(int i=0; i<n/2; i++){
for(int j=0; j<(n+1)/2; j++){
int node = matrix[i][j];
matrix[i][j] = matrix[n-1-j][i];
matrix[n-1-j][i] = matrix[n-1-i][n-1-j];
matrix[n-1-i][n-1-j] = matrix[j][n-1-i];
matrix[j][n-1-i] = node;
}
}
}
};