前段时间火出圈的KAN架构被媒体认为誓要取代MLP成为构建未来AI的基石,我们来一起看看到底怎么回事。
首先KAN的出现肯定是因为目前MLP存在的一些问题:KAN和MLP的区别
1 KAN理论基础
Kolmogorov–Arnold理论,是数学中关于函数逼近的一个重要理论。它主要涉及的是如何用简单的函数来逼近复杂的函数。这个理论的核心思想是,任何连续函数都可以通过一系列简单的操作(如加法和乘法)以及一些基本的函数(如多项式或三角函数)来近似表示。
举个例子:
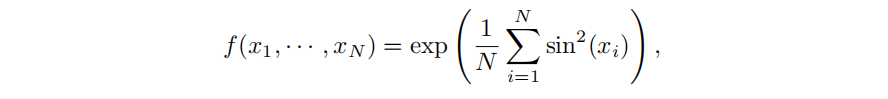
2 经典KAN
KAN和MLP不同,MLP是输入经过线性映射和激活函数,KAN是输入经过样条激活函数再相加,即KAN使用样条激活函数替换了MLP的线性映射+激活函数。
经典的KAN由一个两层网络组成,第一层网络使用N个激活函数处理N个输入,第二层网络使用2N+1个激活函数处理中间2N+1个节点。
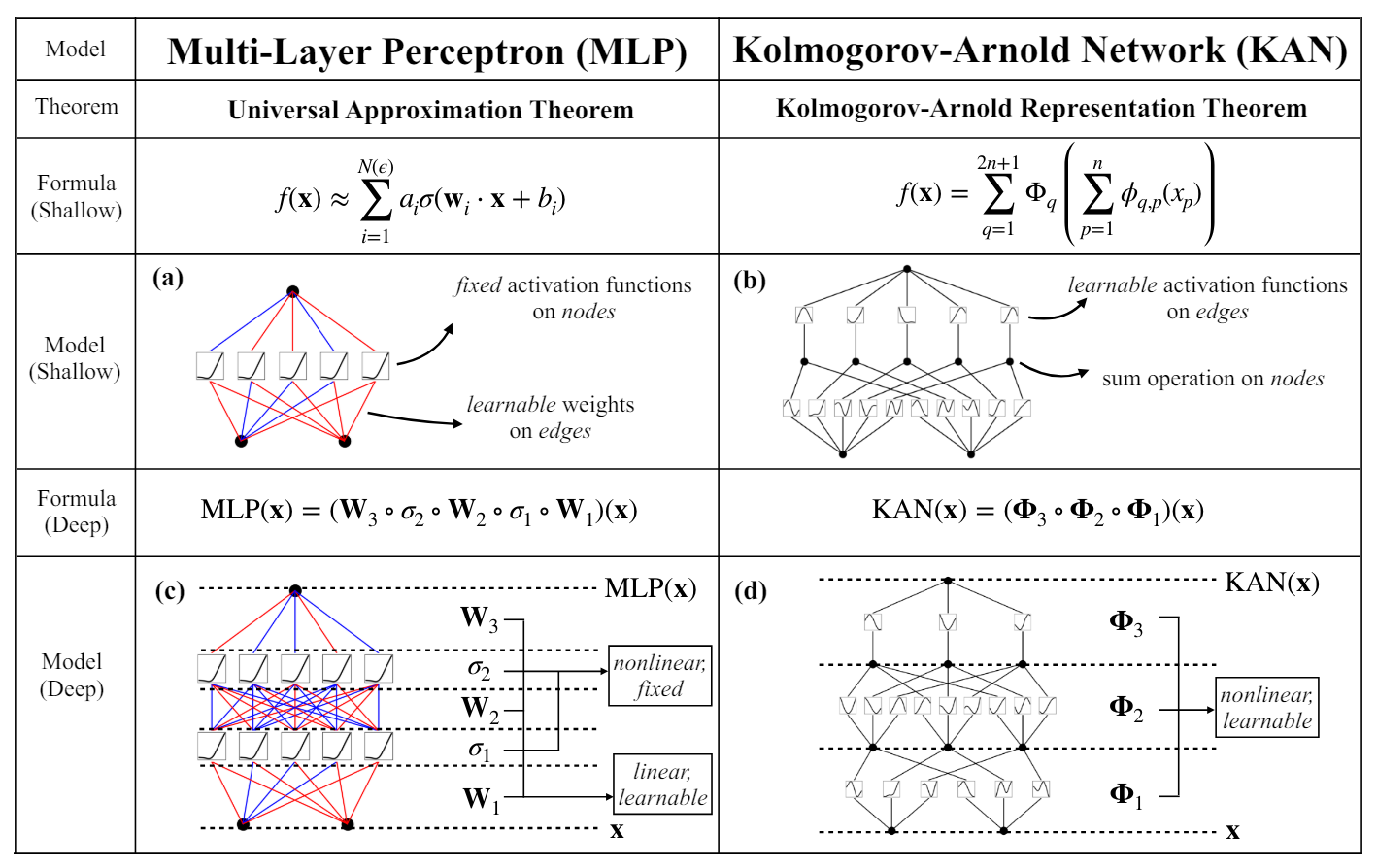
KAN的样条函数的超参有G,G表示样条函数的粒度,G越大表示样条函数更细腻,粒度更小,G越小表示样条函数更粗。因为我们希望刚开始训练时G比较小,训练到后期G更大。

3 泛化KAN
经典KAN是一个两层的Model,但是深度学习引以为傲的是“深度”,如果KAN无法做深,则失去了其价值。
KAN在做深的过程中放宽了KAN理论的限制,不再遵循经典KAN网络中间层激活函数数量为2N+1,而是将中间层全部变成N+1(或者其他)。
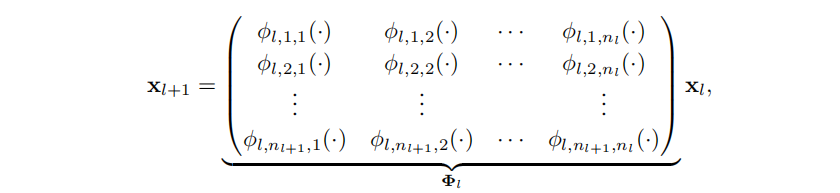
在泛化的过程中实际上和MLP的套路很像,只是MLP权重中的常数变成了样条激活函数。
4 KAN的参数
多层KAN的堆叠已经和MLP基本一致,从简单形式来看参数量是一致的,但是KAN的权重矩阵中每一个样条函数还有一个G的参数.
假设Model Layer为L,隐藏层维度为N,故MLP的参数量为O(N^2*L),KAN的参数量为O(N^2*L*G)。
故实际上KAN的参数量比MLP还要高,但是KAN的复杂度更高,这意味着比MLP更快收敛,在这个算力充分的年代,这都不是事儿。